どうも、ちらです(*’ω’*)
新年初の記事は趣味全開です。
数学的観点から考えたブログの生と死とビジネスについてシンプル化された数理モデルでいけるところまで考えてみました。
最近趣味みたいな記事ばかりになってきてる本ブログですが、今回の記事では
- 「ブログのアクセス数の変化を予測する数理モデルの構築化と考察」
- 「ブログの寿命の予測法とメンテナンスタイミングの同定法」
- 「死に向かうブログを延命する方法 リライトと記事更新がもたらす意味」
などについて扱っていきます。
学部一年生レベルの微分方程式などをガンガン利用していきますが、
わからないところは適宜読み飛ばすなり勉強するなりしましょう。
簡単な文章とyoutube動画ばかり見ていてはダメ!(*’ω’*)←スパルタひよこ🐤
趣味記事なので不勉強な読者はまったりおいていきます!←
でも多分大丈夫。ちゃんと図と日本語解説も多用しております(*’▽’)
ブログのアクセス数の変化を予測する数理モデルを構築する
いきなりですが、もしあなたが今運営しているブログの
アクセス数の変化が予測できる
なんてことになったらとても便利ですよね?(*’ω’*)
自分のブログのアクセス数がどんな伸び方をしてどんな落ち方をするのかがあらかじめわかる。
さらに、その予測モデルを基にしてさらにブログを成長させる施策を打てる。落ちるタイミングを遅らせる。
そんなことができたらうれしいですよね?(*’▽’)
というわけで、今回は未来を予測するための数学”微分方程式”を用いながら
ブログのアクセス数の変化予測モデルをゆるふわと構築します。
微分方程式ってなに?って思った高校生の方などはコチラのPDFを見てお勉強してみるとよいかも?(*’ω’*)
大学の学部一年生レベルの数学を利用しますが、
わからない人やアレルギー体質のある方は日本語解説でふんわり読んでいきましょう。
それではいきましょう\(゜ロ\)(/ロ゜)/
マルサスモデルを利用したブログアクセスの変化予測 ~最も単純なブログの数理モデル~
まず、最も簡単なブログの数理モデルを作ります。
微分方程式を立てるための前提条件について書きますね。
1.ブログのPV数は訪問者数に比例する
2.ブログの訪問者数の変化率はブログに存在する訪問者数に比例する
という条件を満たすとしてお話を進めます(*’▽’)
1.ブログのPV数は訪問者数に比例する
これを数式で表します。PV数をN、訪問者数をx、回遊率をaとすると、
$$N = ax$$
という式が成立します。
2.ブログの訪問者数の変化率はブログに存在する訪問者数に比例する
”ブログの訪問者数の変化率”とは、ブログの訪問者数の時間変化率を意味しています。
例えば、バケツに水を毎秒3mlずつ入れたら10秒後には30mlの水がバケツにたまりますよね?
この時、時間変化率は3ml/sというわけです(速度と道のりと時間の関係と同じです)。
さて、ブログの訪問者数の時間変化率をdx/dt、比例定数rを用いて、
$$\frac{dx}{dt} = rx$$
と表すことができます。
また、ブログの訪問者数の変化率がブログに存在する訪問者数に比例するというのは、
ブログの記事数が増えると検索流入で得られるキーワードが増えていくことに対応しています。
”記事数が増えれば増えるほどブログに人を集められる=訪問者数も増える”
これは感覚的にもわかりますよね?
ただし、本当に訪問者数が記事数の増加に伴い増えるかどうかはわかりません。
ここでは簡単化のために記事数が増加すれば訪問者数も増加するという仮定を置きます(大胆に仮定し、本質をつかむのが数理モデル構築の醍醐味(*’▽’))。
また、比例定数rはブログに入れる記事の質に依存します。
より読まれる高品質な記事を入れることでブログの伸び方は早まります。
この微分方程式は変数分離法という手法で解を求めることができます(サクッと解きます)。
$$\frac{dx}{x} = rdt$$
両辺を積分して、
$$\int\frac{dx}{x} = \int{}rdt$$
$$\ln{x} = rt + C (Cは積分定数)$$
$$x = Ce^{rt}.$$
となります。最後に積分定数Cを消去します。
時刻t=0においてx = x0人の訪問者がいたとすると、C = x0となるので、
$$x = x_0e^{rt}$$
となり、指数関数の形で解が求められます(このような微分方程式は生態系モデルとしても利用され、マルサスモデルと呼ばれます)。
これが最も単純化された数理モデルを用いたブログのアクセス推移の伸び方です。
グラフにするとこんな感じ。
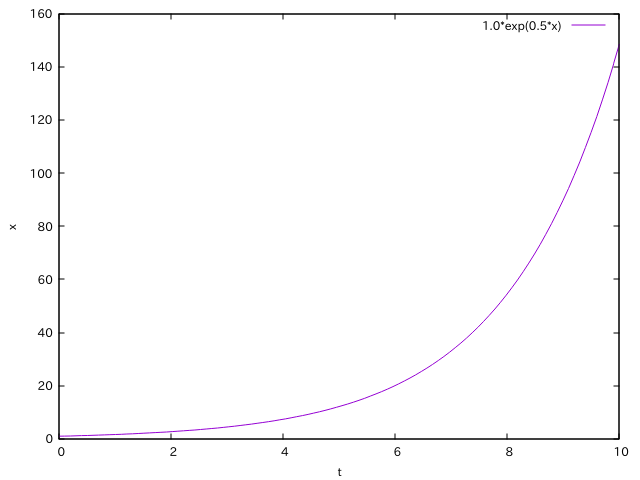
横軸を時間とすると、ブログ訪問者数が指数関数的に退いていくことになります。
なお、ここでは、パラメータとなるx,rはテキトーに選んだので
横軸と縦軸の値自体を現実的なブログ訪問者数の伸び方とは対応させていません。
とりあえずこんな形で伸びていくモデルが作れたんだなあ~って思ってください。
・・・え?(;・∀・)
何してるかさっぱりわからないって?(;・∀・)
(*’ω’*)甘えてるんじゃあない!学部1年生の微分方程式を学ぶんだ!!
おっと。いけない。庭の軍鶏さんが失言してしまったようですね🐤
ひよこのちらさんはそんなこと思ってないからね()
数式は適宜読み飛ばしながら日本語をつかみ取っていくのだ。
とまあ、こんな感じで微分方程式を立ててやれば
ブログの訪問者数の推移を予測する簡易な数理モデルを組み立てられます。
先ほどのモデルでrを変化させてあげるとグラフの形は以下のように変化します。
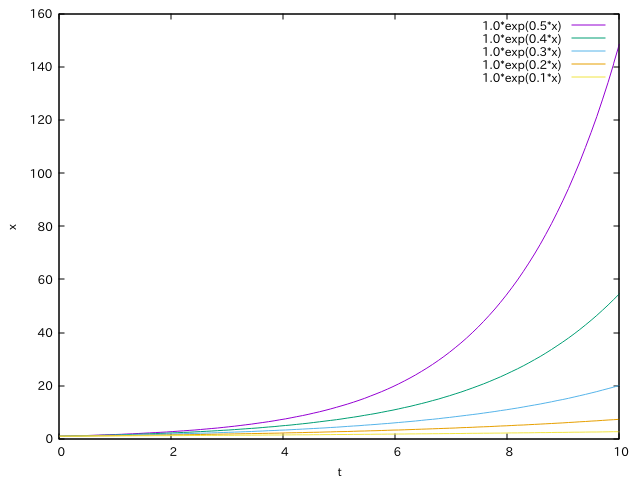
指数関数e^rtの部分のrを変化させるとブログ訪問者数のアクセスの伸び方が変わるわけですね。
比例定数rが大きいほど記事の質が高く、素早く検索上位に上がり、流入数が伸びることになります。
なんとなく実際のブログアクセスの伸び方で見たような形になってきていますかね?(*’ω’*)
でもこれだとず~~っとブログの訪問者数が増えていくことになります。
現実にはずっとブログ訪問者数が伸びていくことはないですよね?
ブログってアクセスが伸び悩む時期があったり、減少したりといった事態も起きますよね?
次はそうしたブログ訪問者数の減少も数理モデルの中に取り入れていきましょう(*’ω’*)
ロジスティックモデルを利用したブログアクセスの変化予測 ~記事腐敗パラメータの導入と結果の考察~
まず、ブログ訪問者数の減少はなぜ生じるのでしょうか?
グーグルのアルゴリズム変動が最も大きな要因として挙げられますね。
他には最近だとグーグルスニペット、グーグルアプリ、YouTubeなど検索0位の存在も見逃せません。
しかし、ここでは複雑な要因をできるだけシンプルに単純化します。
ブログ訪問者数の減少は
・過去に書いた記事が腐敗していくこと
・ライバルの対抗記事に検索順位を抜かれること
に対応していると考えられます。
アルゴリズム変動や検索0位やドメインパワーの弱体化なども上記の二つの中に入りますよね。
ブログに存在する過去記事が集めていた訪問者数は徐々に減少していきます。
こうした現象を取り入れるには、先ほどの微分方程式に記事の腐敗度を導入すればいいわけです。
この記事の腐敗度を追加した微分方程式は
$$\frac{dx}{dt} = r(1-\frac{x}{K})x$$
と表すことができます。
・・・(;・∀・)さっぱりわからないよひよこさん・・・
となっているかもしれないですね(;^_^A
この辺からは少し難しくなりますががんばるんばです!
右辺の形が先ほどのマルサスモデルの形式から変わりましたね(このような形の微分方程式をロジスティック方程式といいます)。
さて、右辺が単なる比例形のrxから変化したわけですが、どういう意味なのでしょうか?
なぜこの式が訪問者数の減少効果を表すのか。最初の微分方程式と一緒に並べてみますね。
$$\frac{dx}{dt} = rx$$
$$\frac{dx}{dt} = r(1-\frac{x}{K})x$$
こんな感じです(‘ω’)ノ
$$(1-\frac{x}{K})$$
この部分の意味をつかむ必要がありますね。
Kはここでは簡単化のためにひとまず定数とします。
もしKが無限大であれば分数は極限的には0になるので、最初の式に戻ります。
しかし、Kが定数であれば訪問者数の伸び方が抑制されることになります。
なぜなら、x/Kが存在することで右辺が単にrxだった時よりも小さな値になるからです。
右辺がrxより小さな値になる。
すなわち、記事の腐敗が取り込まれ、単に記事を入れれば入れるほど訪問者数が増えていくわけ状況ではなくなった。
というわけですね。
記事の腐敗現象を取り込んだ微分方程式を解いていきましょう。
$$\frac{dx}{dt} = r(1-\frac{x}{K})x$$
$$\frac{dx}{(1-\frac{x}{K})x} = rdt$$
$$\frac{Kdx}{(K-x)x} = rdt$$
$$\Bigl(\frac{1}{x}-\frac{1}{K-x} \Bigr)dx = rdt$$
$$\int\Bigl(\frac{1}{x}-\frac{1}{K-x} \Bigr)dx = \int{}rdt$$
$$\ln{\frac{x}{K-x}} = rt+C (Cは積分定数)$$
$$\frac{x}{K-x} = Ce^{rt}$$
$$x = \frac{KCe^{rt}}{1+Ce^{rt}}$$
となります。積分定数Cを求めるために、マルサスモデル同様、t=0でx=x0とすると、
$$x_0 = \frac{KC}{1+C}$$
$$C = \frac{x_0}{K-x_0}$$
となり、xは、
$$x = \frac{Kx_0e^{rt}}{K-x_0+x_0e^{rt}}$$
と解が求められます。
”ブログの訪問者数は既存のブログの訪問者数の数が多いほど増加する”
”ブログ訪問者数は記事が腐敗すればするほど減少する”
という二つの特性を持つ数理モデルが完成しました。
早速図を描いてみましょう。
x0とrは最初のマルサスモデルの時と同じ値にして、K=200としたときの図がこちら。
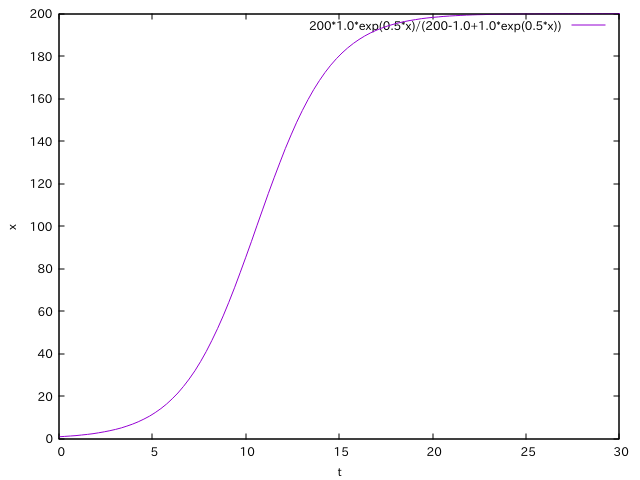
ふむ(*’ω’*)
明らかに最初のモデルとはグラフの伸び方が違います。
同じ図にグラフを描いてみると、
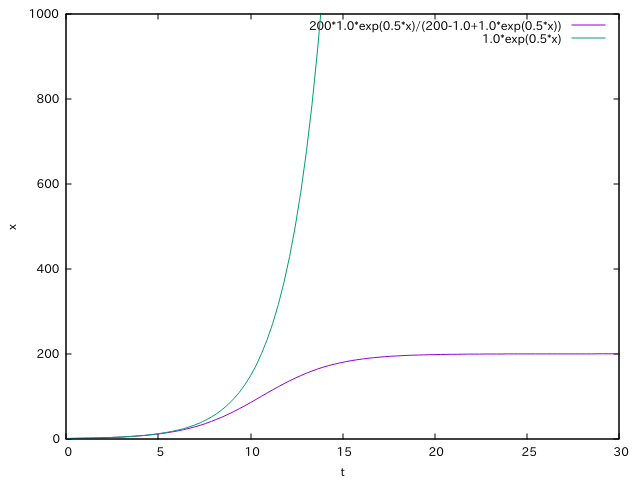
こうなります。
記事の腐敗現象を含まない最初のモデルでは、指数関数的にただただ訪問者数が増加するモデルでした。
が、今回の記事の腐敗現象を含めたモデルではブログ訪問者数は定数Kに漸近していくロジスティックモデルとなりました。
このグラフは必ず定数Kに近づき、またその定数Kを超えることはできません。
すなわち、ブログの記事腐敗速度が大きいほど、アクセス数の頭打ちが早く生じることになります。
記事を入れても入れてもアクセスが伸びない・・・
という声が先輩アフィリエイターさんやブロガーさんから時折聞こえてきますがその理由がこの定数Kの存在にあると考えられます。
この定数Kが大きいほど記事の腐敗度が小さく、アクセスの上限が大きくなることを意味しています。
試しに定数Kを変えたグラフをいくつか描いてみましょう。
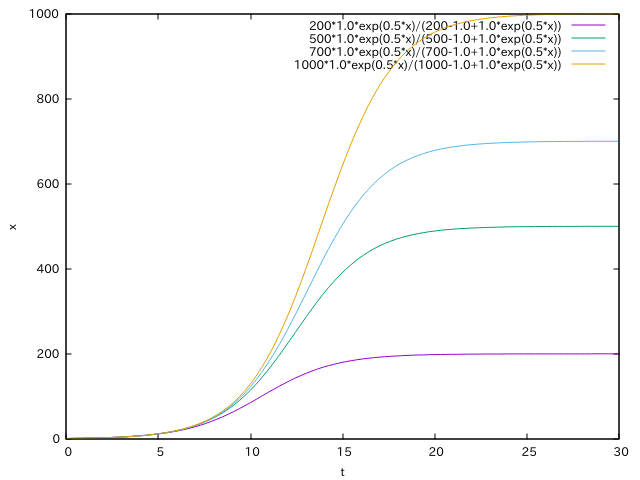
K=200, 500, 700, 1000と変化させたときのグラフを描きました。rやx0は同じままです。
このように、定数Kの値が大きいほど、ブログで獲得できる訪問者数の上限が増加することがわかります(記事の腐敗度が小さくなるので)。
記事の腐敗度に依存してブログの成長度の頭打ちのポイントが決まることがわかります。
さあ、では最後のモデルとして記事更新をやめてしまった場合に何が起こるか考えてみましょう。
ブログの更新を止めると成長時よりも早くアクセス数は減少 ~記事腐敗により死に向かうブログ~
さあ、最後の数式いじりです。
気合を入れていきましょう\(゜ロ\)(/ロ゜)/
とは言え、先ほどのロジスティックモデルを理解できたならもう大丈夫。
次はブログの記事更新をやめ、ただただ訪問者数が減少する死に向かう数理モデルを作ります。
今回の場合は、記事更新をやめてしまうので、ロジスティックモデルの右辺の正の項を消してしまいます。
そして、新しく記事腐敗パラメータbを導入します(このbは本当はKと一緒に扱ってもいいがグラフの傾きだけ変えられるように導入してみた)。
立てる微分方程式は、
$$\frac{dx}{dt} = -br\frac{x^2}{K}$$
です。ロジスティックモデルの右辺の正の項が消滅(記事更新をやめたことを意味している)しています。
では、微分方程式を解いていきましょう。
$$\frac{dx}{dt} = -br\frac{x^2}{K}$$
$$\frac{dx}{x^2} = -b\frac{r}{K}dt$$
$$\int\frac{dx}{x^2} = -\int{}b\frac{r}{K}dt$$
$$x = \frac{1}{\frac{rb}{k}t+C} (Cは積分定数)$$
となり、t=t0でx=x0とすると、積分定数Cは、
$$ x_0 = \frac{1}{\frac{rb}{k}t_0+C}$$
$$ C = \frac{1}{x_0} – \frac{rb}{K}t_0$$
と求まるので、xは、
$$x = \frac{1}{\frac{rb}{K}(t-t_0)+\frac{1}{x_0}}$$
と求めることができる。r=0.5, K=200, t=30でx=199.9とすると、
ほぼ先ほどのロジスティックモデルの後のブログの訪問者数変化を考えたことになる。
記事腐敗パラメータbを1.0とすると(bを変化させるとグラフの傾きが変わります)、
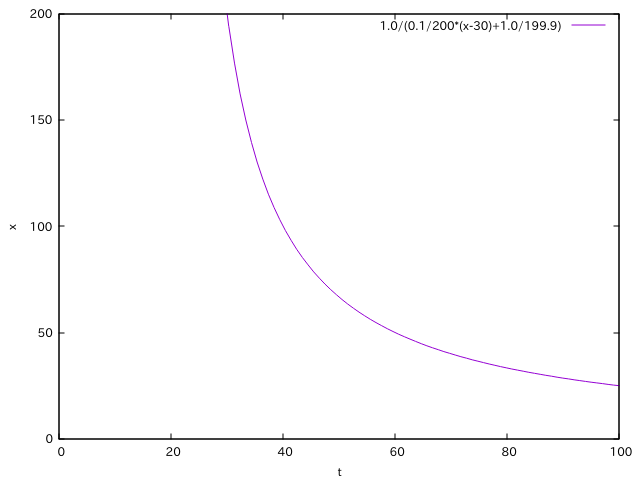
このように、反比例型のグラフとなり、訪問者数xが単調減少することがわかる。
また、先ほどのロジスティックモデルの解とつないでみると、以下のような図となる。
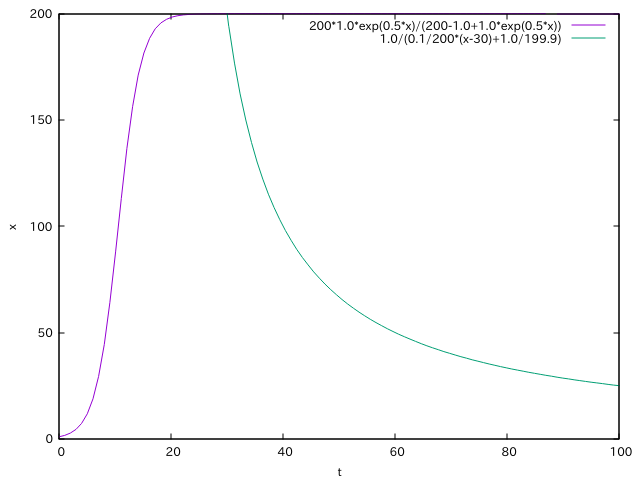
これがブログの訪問者数の増加から減少までの時間推移、
すなわち理想化されたブログの生死を表す数理モデルとなります。
ロジスティックモデルと記事腐敗モデルを合わせてBlog Life-and-Death Modelと名付けましょう!(*’ω’*)←あふれる厨二感
え・・・?(‘◇’)ゞ
ただロジスティックモデルと減衰型の解を持つ微分方程式を積分区間分けて解つないだだけだろって?(‘◇’)ゞ
その通りです!(*’ω’*)←
しかしこんな単純化したモデルでもそれっぽい議論ができるのが面白いと個人的には思ってるのでこのままいきます!笑
もちろん、このモデルがすべてのブログの生死を説明するなんて言うつもりはないです。
こんな風に単純化した模型で考えてどこまで掘り下げられるかを考えるのが楽しい・・・でしょ?(*’ω’*)←
厳密性をどうこう言うものではないのです(数値代入も実際テキトーな値ですし)。
さてさて、Blog Life-and-Death Modelが表すブログの生死の流れは以下。
1.ブログ誕生。最初記事数があまり入っていない時は訪問者数の伸びは遅いが、
ある程度記事が集まると、どんどんブログに訪問者が集まる。
2.ある程度記事数が増えると、今度は記事の腐敗が始まり、既存記事への訪問者数の減少が効くようになる。
3.最終的には記事を入れることによる訪問者数の増加と記事が腐ることによる訪問者数の減少がバランスする。
その最終訪問者数が定数Kにより定められる。
4.最後に、人は記事更新をやめてしまい、記事の腐敗のみが残り、訪問者数が激減してブログは死に向かう。
どうでしょうか?(*’ω’*)
なかなかそれっぽいグラフになっていると思いませんか?
かなり理想化された簡単な数理モデルではありますが、ブログの生死をうまく説明してくれていると思います。
このモデルから得られる特徴として面白い部分がいくつかあるので解説していきます。
ブログは育つまで時間がかかるけど死ぬのは一瞬。実はグラフの傾きから一目瞭然だった!?
「ブログやサイトは人がやってきて育つまで時間がかかるものの、アクセスがなくなり死んでしまうのは早い・・・
だから、サイトを複数運営してリスクヘッジしないといけないんだ!」
なんてお話を聞いたことはありませんか?(*’▽’)
もしくは自分自身でこの状況を体験した人もいるかもしれないですね。
どうしてブログは育つのに時間がかかるのに死んでしまうのはすぐなんだろう?
実は、こんなこともBlog Life-and-Death Modelから得られる結果を見ると原因を考察することができるのです!
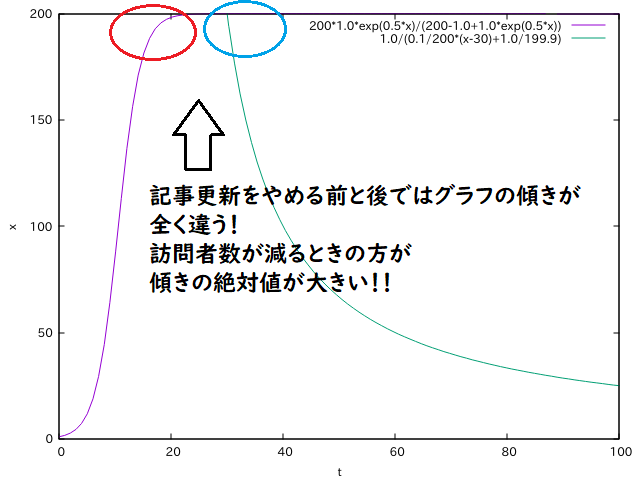
結論をもう図に書いちゃいました笑
記事更新をやめる前のロジスティックモデルとやめた後の記事腐敗モデルではグラフの傾きの大きさが異なるのです(‘Д’)
ロジスティックモデルで訪問者数の上限パラメータKに近づくときはゆるやかな傾きですが、
記事腐敗モデルにおいては傾きの絶対値が最も大きくなるのが記事更新をやめた直後なので一気に訪問者数が減少してしまうのです。
ブログの更新をやめてしまうと一気にアクセス数が落ちてしまった・・・
なんてことも数理モデルにちゃんと取り込まれています(*’▽’)
ブログの寿命を予測するための手立て カギとなるワードは”変曲点”
では、次にブログの寿命を予測する方法はないのかを考えてみましょう(*’ω’*)
Blog Life-and-Death Model(定着させるぞっ🐤)のロジスティックモデル部分を見ると実は寿命を予測するための手がかりを得ることができます。
その手がかりが”変曲点”です。
変曲点とは、二階の導関数の符号が変化する点のことを言います。つまり、グラフの傾きの変化率の符号が変わる点です。
もっとわかりやすく言うと、ブログ訪問者数の伸びが衰え始める点です。
ロジスティックモデル部分において、訪問者数の変化率(つまりxに関する一階の導関数)は、
$$\frac{dx}{dt} = r(1-\frac{x}{K})x$$
で表されるので、もう一度微分してあげると、
$$\frac{d^2x}{dt^2} = r(1-\frac{2x}{K})$$
となります。この値が0の場所が変曲点なので、x=K/2のところでブログの訪問者数の変化率の増え方が衰え始めます。
これはグラフを見ても確かにそうなっています。
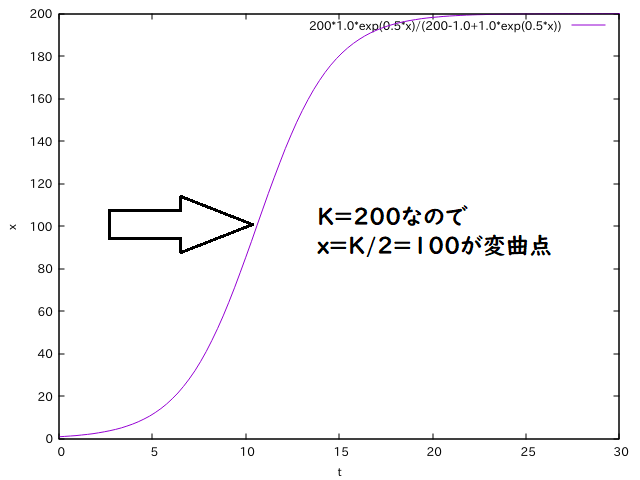
つまり、変曲点を観測したらブログの伸び盛りの時代を終えようとしているということ。
さらなる成長のためには新しい記事をもっと入れたり、後述するリライトによる補強や被リンク施策などを行っていく必要があります。
ブログのアクセス数を月毎にプロットし、そのアクセス数の変化率の伸び方が落ち始めたところ。
ここが見えたらブログの寿命が近づき始めている・・・なんて考え方もできるかもしれませんね(*’ω’*)
また、この点はロジスティックモデルにおいてはなんとも都合のいい値K/2となっています。
そう!変曲点にはブログのアクセス数の上限値を意味するKが入っています!!(*’▽’)
つまり・・・変曲点を捉えた地点の約二倍がそのブログのアクセス数の天井というわけです。
実際にブログを育成していく上でどのへんまでブログが成長するかを先に知ることは極めて困難です・・・が、
ロジスティックモデルがある程度成立すれば変曲点を観測した地点でそのブログを運営することで得られるPVの最大値を知ることができます。
もちろん、理想化された数理モデルなので必ずしも成立するわけではない(というより基本的にはこんなきれいに成立するわけないww)ですが、もし成立したら面白いですよね?^^
自分のブログの伸びしろが早い段階でわかるわけですから(*’▽’)
逆に、ブログの天井が見えてきたところで新たな施策を施し、アクセス数の天井を上げることができたら素敵です(‘ω’)ノ
ブログの寿命を延ばすための方法 記事を入れるorリライトが必要な理由を数理モデルから解き明かす
ここまでで、ブログの生死の数理モデルの構築やそこから読み解かれるブログあるあるな事象を解説してきました。
また、変曲点を迎えたところからブログの寿命が近づいていることを読み取ることができましたね(もちろん数理モデルが成立するなら・・・です笑)。
次によくブロガーさんやアフィリエイターが言う
・ブログを成長させるならどんどん記事を入れろ。たくさん質がいい記事を入れろ
・ブログは書いたら書きっぱなしではなくリライトせよ
なんてことについてもBlog Life-and-Death Modelで考えてみましょう!(*’ω’*)
$$\frac{dx}{dt} = r(1-\frac{x}{K})x (0\leq{}t\leq{}t_0)$$
$$\frac{dx}{dt} = -b\frac{x^2}{K} (t_0\leq{}t)$$
(t=t0からブログ記事更新をやめたとする)
これら二つの式においてパラメータr,K,bはこれまで定数として扱っていましたが、
ブログの更新法を変えたりリライトを入れるということがパラメータを変化させることに対応すると考えられます。
・ブログを成長させるならどんどん記事を入れろ。たくさん質がいい記事を入れろ
まず、ブログを成長させたいなら記事をどんどん入れろ。質がいい記事をたくさん入れよう。
こんな話をよく耳にします。
・ブログに記事をどんどん入れる = rの値を高める効果
・記事の品質を上げる = rの値を高める&Kの上限値を高める効果
rが大きければ大きいほどブログの訪問者数が伸びる速度が高まります。
これは検索上位に入る記事が増えていく速度に対応しますね。
ただし、グーグルにフェッチされて記事評価される速度が律速(速さを制御するボトルネック・キーになるパラメータ)になるはず。
そのため、ある程度までしかrを上げることはできないでしょう。
ただし、中古ドメインを使うとこのrに対してドーピングをかけることができる気がしますね・・・(*’▽’)
でも被リンクまで考慮するのは難解なので今回の記事では除外します。
また、検索上位にいる記事が多いという状況を実現させるのは”記事の品質”とライバルの”記事の強さ”の相対関係です。
パラメータKはこうした記事の検索順位に関する複雑性が詰め込まれた簡易パラメータと考えることができるでしょう。
そのため、記事の品質を上げることはブログの訪問者数の上限値であるKの値を増加させることになります。
質のいい記事を早く書いていくことがブログの速やかな成長には不可欠ということですね。
・ブログは書いたら書きっぱなしではなくリライトせよ
さあ、次はブログ更新で大事だといわれるリライト=記事のメンテナンスに関する考察です。
このリライトにより、古くなった記事を最新の状態にしたり、
抜かれたライバルの記事をさらに抜き返すなどの効果があります。
すなわち、パラメータKの値を高め、同時に記事腐敗パラメータbを減少させる効果があると考えられます。
記事のリライトを行うことで、
ブログの最終的なアクセス上限値を高め、記事腐敗速度を減少させることができるでしょう。
実力あるブロガーさんが”記事をリライトしろ”
と口酸っぱくして言うのはトイモデルの範囲では妥当性があるように感じられますね(*’ω’*)
現実のブログのアクセス推移との比較 有名ブログと無名ブログをピックアップして理論と比較!
最後にいくつか実際のブログの生死や成長過程のデータを観測してみました。
人はデータを得ても見方を知っていないと見ることはできない
今回の数理モデルで得た見方を念頭において実測値の観察を楽しんでみましょう(‘ω’)ノ
アクセス数を観測する実験器具としてはAhrefsを利用。
記事アクセスの絶対値はそこまで信用できませんが、相対的なグラフの推移は信用できると考えています。
理論を作って考察したら現実と比較。どの程度までうまく説明できてるのか。
また、数理モデルが成立するならどのように解釈していけばいいのかを試してみましょう(‘ω’)ノ
例1.一時期はがっつり更新していたが急に更新をやめた雑記ブログ
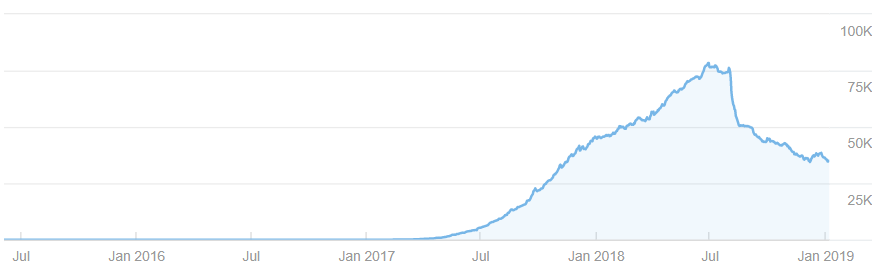
こちらは2018年の7月までがっつり更新していた雑記ブログですね。
夏からは全然記事が更新されていません。
Blog Life-and-Death modelから得られた知見から考えると、
ロジスティックモデルの途中過程で記事更新を停止し、記事腐敗の効果のみが働いたと考えられます。
グラフの動きを細かく数理モデルに合わせてフィッティングまではやりませんが概ね理論の挙動と一致していますね^^
例2.記事品質がそこまで高くないが運営歴が長い季節性トレンドブログ 2018年夏から更新なし
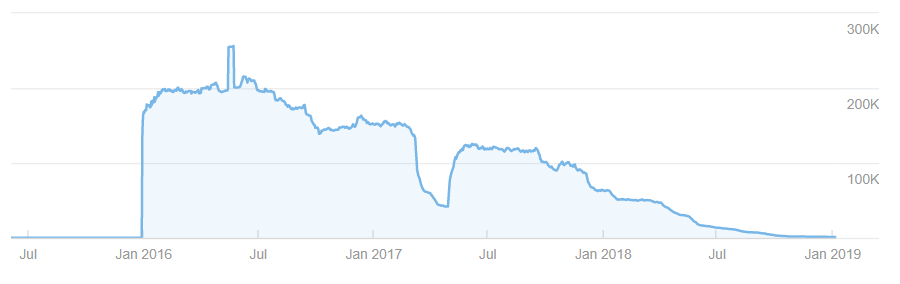
こちらのブログはとある季節性トレンドブログです。
一時はウハウハになるようなアクセスの伸びを見せていたようですね。
ただ、記事の品質はそこまで高くなく、
狙っているキーワードをグーグルで検索すると同じようなタイトルの記事がずら~~っと並びます。
ひな祭り 地域名 ○○みたいな季節性と地域性がメインキーワードの記事が多いブログでした。
ライバルが真似しやすく横展開までの発想もいらないため、
徐々に記事の質や文字数攻めされて記事腐敗を止めることができなかったと考えられます。
更新をしていても記事の品質が低ければどんどんKの値が落ちてしまい
ロジスティックモデルの上限値が下がってくると考えられます。
例3.アドセンス特化型ブログ絶賛更新中
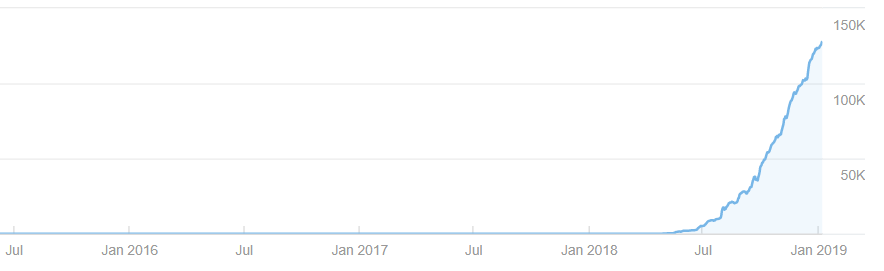
次はとあるアドセンス特化ブログです。
こちらのブログはうまくライバルが少なく、かつ検索数も多いジャンルを多数の記事で殴りに行っています。
非常に順調な伸び方をしており、まだ記事腐敗の挙動が現れていませんね。
例4.アドセンス特化型ブログ更新なし
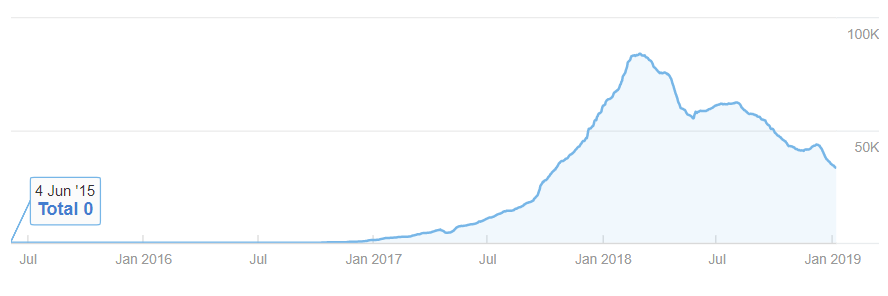
こちらは2018年2月から記事更新をやめている特化型アドセンスブログです。
かなりうまく理論に乗っかってる気がしますね(‘ω’)ノ
立ち上がりはrが小さめでしっかりアクセスを伸ばす。
そして記事更新をやめた2018年2月を境にして挙動が変わり、記事腐敗が支配的となっています。
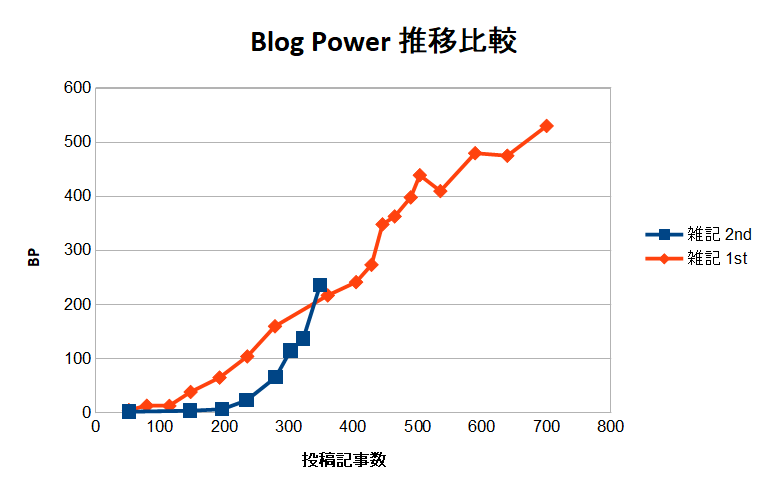
例5.最強形態と思われる鬼リライト型アドセンスブログ
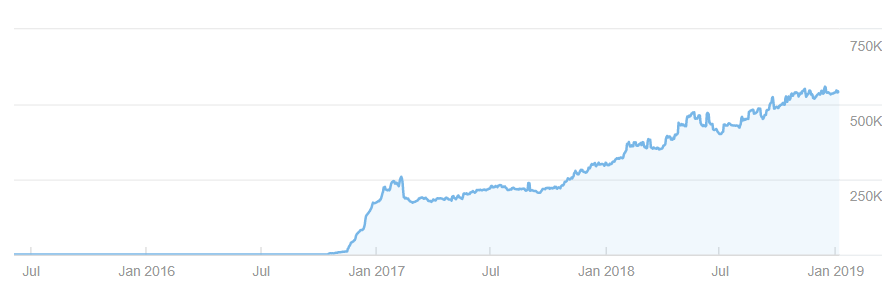
このブログはこれまでとブログの運営法が異なります。
高い記事品質と高いリライト頻度で運営。見ての通りアクセス数の桁が違う超強力なブログです。
このブログは2017年度半ばで一度アクセス数の最大値を迎えていますが、
その後もリライトと記事更新によりブログ訪問者数の上限値を与えるKの値を上昇させ、
記事腐敗パラメータbを限りなく小さな値に抑え込んでいます( ゚Д゚)
1記事1記事が精鋭部隊であり、
かつ腐らせないリライト戦略をとっている理想的な運営スタイルのブログです。
例6.某ブロガーさんのブログアクセス推移1
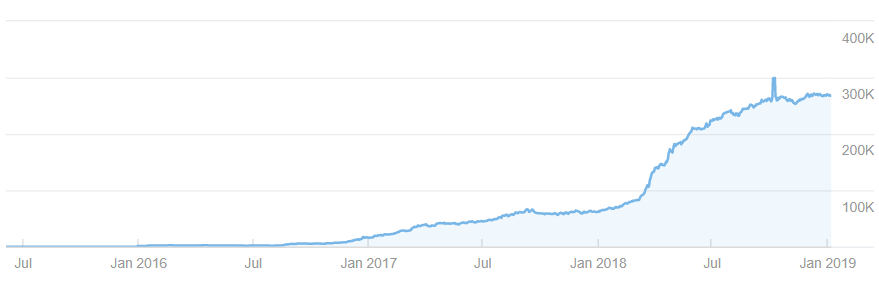
ツイッタランドの某ブロガーさんのブログのアクセス推移です。
しっかり記事が更新されており、記事腐敗速度を常に追い抜いています。
最近はロジスティックモデルの頭打ちとなる上限値Kの値にやや近づき始めている気がしますね。
しかしこのブログはアクセス上限付近にいたと思わせてまた再上昇した過去を持つのでまだどうなるかわかりませんね。
このあと記事腐敗が勝つのか・・・それとも?(*’ω’*)
例7.某ブロガーさんのブログアクセス推移2
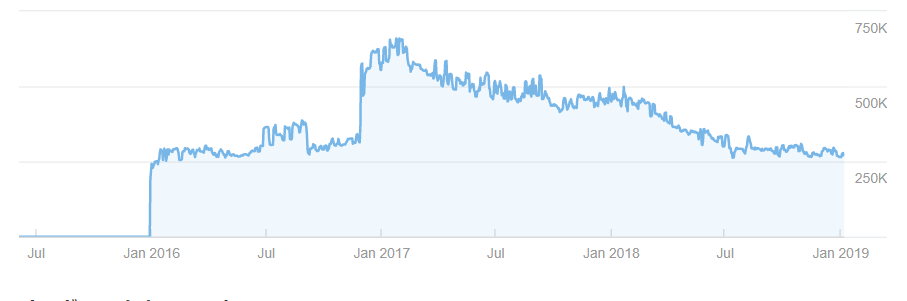
こちらのブログはなんとも独特な伸び方をしています。
また、これまでとは異なり、アクセスの伸びる箇所が定期的にインパルス応答的に発生しています。
さて、なぜだと思われますか?(*’ω’*)
実はこのブログはSNS流入で爆発力があるブログです。
恐らくですが、インパルス応答はSNSでバズったときの応答だと考えられます。
ブログの記事更新数が衰えてきているので記事腐敗モデルが支配的になりつつありますね。
さて、このままブログは死んでしまうのか・・・それとも・・・?
例8.SNSによるインパクトが絶大すぎるブログ

こちらのブログは超特殊。記事更新直後のSNS流入がえげつない。
グラフの乱れ方が常軌を逸しています笑
記事更新時にどれだけ固定ファンから流入してるんですかwwって感じです。
SNSによるバズり・拡散効果の影響度が大きく、数理モデルの適用範囲を完全に超えてしまっていますね(;・∀・)
インパルス応答部分をノイズと考えて除外したと考えればある程度は数理モデルっぽい動き・・・か?汗
例9.某ブロガーさんのブログアクセス推移3

堅実な伸び方をしている某ブロガーさんのブログアクセス推移です。
2018年の6月前後で記事の更新法を変更したのでしょうか?
曲線の傾きが急激に上昇し、一気に読者数上限値パラメータKに到達してる感じがします。
そこからもコツコツと記事を書き溜め、定期的なバズを起こしながら順調にアクセス推移を伸ばしていますね。
このブログもSNS流入がかなり大きいのでなかなか数理モデルに素直に乗っかってこないんですかね・・・
・・・(*’ω’*)
以上、勝手に人のブログをahrefsで観察して数理モデルで得た観点でアクセス推移を眺めてみるお時間でした笑
当たり前ですが数理モデルはめちゃくちゃシンプル化して考えてますし、
あの数式の形でいいかという妥当性もありません。めちゃくちゃいい加減なモデル化です(*’ω’*)←
ですが、大域的な挙動はBlog Life-and-Death modelに乗っかってきてる部分もあるのかなって思います。
あなたはどう思います?
粗いモデルと考察ではしたが意見もらえたら喜びます(*’ω’*)
SNS流入力が強いブログはKの値を強く押し上げているのも印象的でした。
検索流入以外からの集客法を持っているとかなり変わった挙動を起こせるのでしょうね。
一過性の流入がブログのドメインを強化し、アクセス数を伸ばすのに寄与するというお話もありますが、
そのあたりが現れているのかもしれないですね。
さて、大分長くなってしまったので最後に軽くまとめて終わりにしましょう(*’ω’*)
まとめ
ブログのアクセス推移を簡単な仮定と単純な数学により数理モデルで定性的に表現してみました(*’ω’*)
ロジスティックモデル+記事腐敗モデルを合わせて解いてあげることで
定性的なブログの生死と運営手法がもたらす意味がつかめました。
$$\frac{dx}{dt} = r(1-\frac{x}{K})x (0\leq{}t\leq{}t_0)$$
$$\frac{dx}{dt} = -rb\frac{x^2}{K} (t_0\leq{}t)$$
なお、時間t、ブログ訪問者数x、記事の成長率を意味するパラメータr、読者数上限数を意味するパラメータK、記事の腐敗速度を意味するパラメータbとする。
ブログアクセス数Nは
$$N = ax$$
で表される(aはブログの回遊率を表す定数)。
解は、
$$x = \frac{Kx_0e^{rt}}{K-x_0+x_0e^{rt}} (0\leq{}t\leq{}t_0)$$
$$x = \frac{1}{\frac{rb}{K}(t-t_0)+\frac{1}{x_0}} (t_0\leq{}t)$$
で表現される。
・ブログは立ち上がりに時間がかかるが、記事更新をやめてから死ぬまでの速度は速い(グラフの傾きの立ち上がりと落ち方に明確な差が存在する)。
・新規記事を導入する=ブログ成長率rの値の維持&上昇、読者数の上限値Kを高める作用
・記事をリライトする=読者数の上限値Kを高め、ブログ腐敗度bを下げる作用
・x=K/2の変曲点を観測できればそのままの手法でブログを育成したときのアクセス数の天井がわかる・・・かも?
・ここまでの数理モデル形成は大胆かつシンプルな仮定を課しているため、定量的な数学的正当性は本来論じえない
以上で新年初の趣味全開記事を終わります!(*’ω’*)
こんな個人の嗜好に全振りした記事を読んでいただきありがとうございましたああぁぁ!!


コメント
はじめまして。コメント失礼いたします。
工学部の化学科で数学キライなので、基本的に数式モデルはキライ派です。
(実際にやってみないとわからないだろう by 化学工学)
ですが、興味深く拝見させていただきました。
ブログは資産記事とトレンド記事で区別する場合もあると思いますが、今回のモデルはどちらかというと、アドセンス狙いのトレンド記事寄りのモデルということでしょうか?
記事の寿命は資産記事とトレンド記事で多少違いがあると感じていて。
(まあ、結局のところ、係数の大きさの違い…なのでしょうか?)
資産記事もそんなに崩壊していくのだとしたら、サイト運営はなかなかえげつないと感じたので、興味本位で連絡した次第です。
松坂さん
コメントありがとうございます!^^
そしていきなりバサッと切ってもらえておお( ゚Д゚)ってなってます。
現実肌や工学系の人はこういう定性モデルはいい加減だから嫌いってなること多いですよね笑
学会でも経験済みですが僕としてはこのタイプの研究は現実に合うかにはあまり重きを置いてなくて、ものの見方を提起しているという感覚です(*’ω’*)
ご推察通り基本的には検索流入SEO重視のトレンドブログを念頭に置いています。
ただ、思ってたより資産ブログでもつぶれていくものもあるんですよね。
同じ資産ブログでもサイトの設計だったりリライト頻度などによって係数の大きさが変わると考えています。
狙うクエリーに群がる競合にも大きく依存しているでしょう。
記事書いて放置は実際にはほぼほぼ下がるのだろうと考えていますね。
うまくサイトの設計をやれば寿命は伸ばせる。さらに、リライトなどメンテナンスを入れてパラメータ調整を行って上げる必要があるのかなと。
大規模サイトの複数運営は現実的ではないという方もおられるのでえげつないという感覚は案外間違っていないかもしれませんね(;・∀・)
でも在宅でできて、固定費はほぼなし。利益率超高いビジネスである程度放置性も効くので個人事業としてはやはりアリだと思いますね^^
見返したら思ったよりきつい文面になっていますね、申し訳ありません。
もともと数学がニガテなこともあって、キライ笑 程度のニュアンスです٩(ˊᗜˋ*)و 笑
ブログ寿命に関して、感覚的だったスピード感が数式化されていて、とても興味深く拝見させていただきました。
確かに、競合サイトのクオリティの向上に伴って、相対的に記事の価値が下がるという側面もありますね。納得です。
ご丁寧に返信頂きまして、ありがとうございます。